Už dávno som videl v TV jeden dokument, kde sa pojednávalo o časopriestore a vysvetľovalo sa ako plynie čas objektom, ktoré sú voči iným objektom v pohybe. Pri veľmi malých rýchlostiach (napr. stanica ISS sa pohybuje rýchlosťou približne 27 500 km/h, čo je prvá kozmická rýchlosť) nemá význam ani hovoriť. Čo som sa dočítal v 100+1, tak najvyššia rýchlosť bola dosiahnutá sondou New Horizons a to 58 536 km/h. Toto sú oproti rýchlosti svetla zanedbateľné rýchlosti.
Časová dilatácia je fenomén, kde čas plynie pomalšie pre objekt, ktorý sa pohybuje veľmi vysokou rýchlosťou (blížiacou sa rýchlosti svetla) v porovnaní s objektom, ktorý je v pokoji alebo sa pohybuje pomalšie. Tento jav bol experimentálne potvrdený mnohokrát, napríklad v experimentoch s rýchlo sa pohybujúcimi časticami alebo pomocou atómových hodín na lietadlách.
Predstavme si rýchlosti, ktoré by aspoň z polovice dosahovali rýchlosť svetla . Ak by existoval dopravný prostriedok (nazvime ho raketa), ktorý by sa pohyboval tesne nad zemou rýchlosťou 149896,229 km/s (čo je polovica rýchlosti svetla) a obiehal by okolo zeme. Ak by do rakety nastúpil Bob a povedal by Alici, že sa ide trocha povoziť, nech ho počká presne 5 minút. Alica by ho čakala, ale Bob by neprichádzal. Ak by Bob nakoniec s raketou zastavil, tak Alica by mu odvrkla „Bob veď ty ani nevieš odčítať 5 minút„! Bob by jej povedal, nech sa sama naučí odčítavať čas z hodiniek. Je vôbec možné, aby Bob, alebo Alica nevedeli odčítať čas z hodiniek ? Jeden z nich sa musel predsa pomýliť. Poďme sa pozrieť na to, kto pochybil.
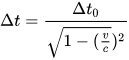
- Δt – čas na plynúci zemi
- Δt0 – čas plynúci v rakete
- v2 rýchlosť rakety
- c2 rýchlosť svetla vo vákuu (299792,458 km/sň
Ak si do vzorca dosadíme správne hodnoty, tak dostaneme veľmi zaujímavé čísla. Čas Δt0 premeníme na sekundy. Rýchlosti km/s sa vykrátia a zostane nám výsledok v sekundách:
300/(√(1-(149896,229/299792,458)^2 = 346,410161514 sek 50%
300/(√(1-(224844,3435/299792,458)^2 = 453,557367611 sek 75%
300/(√(1-(269813,2122/299792,458)^2 = 688,247201612 sek 90%
300/(√(1-(296794,53342/299792,458)^2 = 2126,643615025 sek 99%
300/(√(1-(299492,665542/299792,458)^2 = 6709,881612639 sek 99,9%Z výpočtov vyplýva, že čas správne odčítal Bob, ale aj Alica. Bobovi v rakete uplynulo 5 minút a Alici uplynulo na zemi 5 minút a 46 sekúnd Výpočty som ešte spravil pre ďalšie rýchlosti. Pokračoval som na 75% rýchlosti svetla, nasledovala rýchlosť 90%, 99% a 99,9%. Pri rýchlosti 99,9% sa čas na zemi už podstatne líši od času v rakete. Z výpočtov vyplýva, že ak by Bob nastúpil do rakety o 12:00 a vystúpil by z nej o 12:05, tak Alica by už na svojich hodinkách mala 13:52. To znamená, že Bob by bol od Alice mladší o 1 hodinu a 47 minút.
Ospravedlňujem sa odbornej verejnosti, keď som fenomén dilatácie času zle vysvetlil, alebo nebodaj som sa pri výpočtoch pomýlil. Informácie som čerpal z internetu, ktoré som si inde neoveroval.
